本文共 6847 字,大约阅读时间需要 22 分钟。
iptables防火墙
一.iptables概述
- linux系统的防火墙:IP信息包过滤系统,它实际上由两个组件 netfilter 和 iptables 组成
- 主要工作在网络层,针对IP数据包。体现在对包内的IP地址、端口等信息的处理上。
二.netfileter/iptables 关系
-
netfilter:属于“内核态”(kernel space, 又成为内核空间)的防火墙管理体系。
-
iptables属于“用户态”(User Space,又称为用户空间)的防火墙管理体系。
是一种用来管理Linux防火墙的命令程序,它使插入、修改和删除数据包过滤表中的规则变得容易,通常位于/sbin/iptables目录下。 -
netfilter/iptables后期简称为iptables。
iptables是基于内核的防火墙,其中内置了raw、mangle、nat和 filter 四个规则表。表中所有规则配置后,立即生效,不需要重启服务。
三.四表五链
- 规则表的作用:容纳各种规则链
- 规则链的作用:容纳各种防火墙规则
- 总结:表里有链,链里有规则
1. 四表
- raw表:确定是否对该数据包进行状态跟踪。包含两个规则链,OUTPUT、PREROUTING
- mangle表:修改数据包内容,用来做流量整形的,给数据包设置标记。包含五个规则链,INPUT、OUTPUT、FORWARD、PREROUTING、POSTROUTING
- nat表:负责网络地址转换,用来修改数据包中的源、目标IP地址或端口。包含三个规则链,OUTPUT、PREROUTING、POSTROUTING。
- filter表:负责过滤数据包,确定是否放行该数据包(过滤)。包含三个规则链,INPUT、FORWARD、OUTPUT。
注:在 iptables 的四个规则表中,mangle 表和 raw 表的应用相对较少。
2.五链
-
INPUT:处理入站数据包,匹配目标IP为本机的数据包。
-
OUTPUT:处理出站数据包,一般不在此链上做配置。
-
FORWARD:处理转发数据包,匹配流经本机的数据包。
-
PREROUTING链:在进行路由选择前处理数据包,用来修改目的地址,用来做DNAT。相当于把内网中的80端口映射到路由器外网端口上。
-
POSTROUTING链:在进行路由选择后处理数据包,用来修改源地址,用来做SNAT。相当于内网通过路由器NAT转换功能实现内网主机通过一个公网IP地址上网。
3. 数据包到达防火墙,规则表之间的优先顺序:
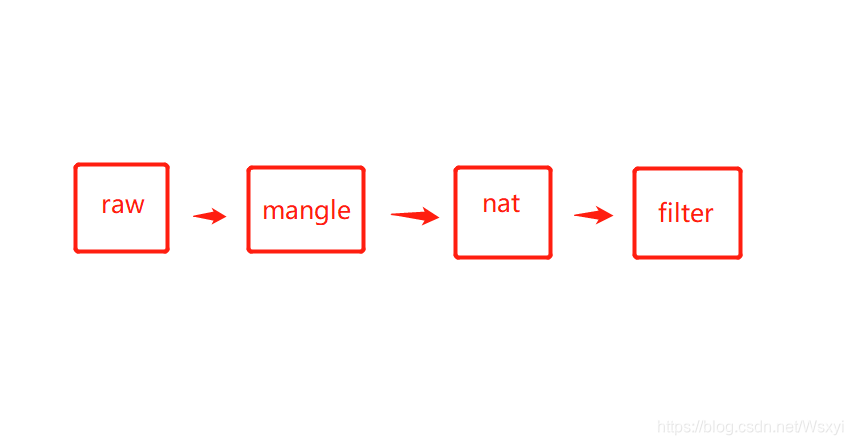
4.规则链之间的匹配顺序
-
主机型防火墙:
入站数据(来自外界的数据包,且目标地址是防火墙本机):
PREROUTING—>INPUT—>本机的应用程序
出战数据(从防火墙本机向外部地址发送的数据包):
本机的应用程序----> OUTPUT---->POSTROUTING-
网络型防火墙:
转发数据(需要经过防火墙转发的数据包):PREROUTING---->FORWARD---->POSTROUTING
-
规则链内的匹配顺序:
自上向下按顺序依次进行检查,找到相匹配的规则即停止(LOG策略例外,表示记录相关日志)
若在该链内找不到相匹配的规则,则按该链的默认策略处理(未修改的状况下,默认策略为允许)
四.iptables 的安装
- Centos 7默认使用firewalld防火墙,没有安装iptables,若想使用 iptables防火墙。必须先关闭firewalld防火墙,再安装iptables
------关闭firewalld防火墙:systemctl stop firewalld.servicesystemctl disable firewalld.service------安装并开启iptables服务:yum -y install iptables iptables-servicessystemctl start iptables.service

五.iptables 命令行配置方法:
1.命令格式:
命令格式:iptables [-t 表名] 管理选项 [链名] [匹配条件] [-j 控制类型]
2.注意事项:
- 不指定表名时,默认指filter表
- 不指定链名时,默认指表内的所有链
- 除非设置链的默认策略,否则必须指定匹配条件
- 选项、链名、控制类型使用大写字母,其余均为小写
3.常用的控制类型
| 控制类型 | 作用 |
|---|---|
| ACCEPT | 允许数据包通过 |
| DROP | 直接丢弃数据包,不给出任何回应信息 |
| REJECT | 拒绝数据包通过,会给数据发送端一个响应信息 |
| SNAT | 修改数据包的源地址 |
| DNAT | 修改数据包的目的地址 |
| MASQUERADE | 伪装成一个非固定公网IP地址 |
| LOG | 在/var/log/messages文件中记录日志信息,然后将数据包传递给下一条规则。LOG只是一种辅助动作,并没有真正处理数据包。 |
4.常用的管理选项
-A :在指定链的末尾追加(–append)一条新的规则
-I :在指定链的开头插入(–insert)一条新的规则,未指定序号时默认作为第一条规则
-R :修改、替换(–replace)指定链中的某一条规则,可指定规则序号或具体内容
-P :设置指定链的默认策略(–policy)
-D :删除(–delete)指定链中的某一条规则,可指定规则序号或具体内容
-F :清空(–flush)指定链中的所有规则,若未指定链名,则清空表中的所有链
-L :列出(–list)指定链中所有的规则,若未指定链名,则列出表中的所有链
-n :使用数字形式(–numeric)显示输出结果,如显示 IP 地址而不是主机名
-v :显示详细信息,包括每条规则的匹配包数量和匹配字节数
–line-numbers:查看规则时,显示规则的序号
六.使用iptables
1.添加新的规则:
iptables -t filter -A INPUT -p icmp -j REJECTiptables -I INPUT 2 -p tcp --dport 22 -j ACCEPT
2.查看规则列表:
iptables [-t 表名] -n -L [链名] [--line-numbers]或iptables -[vn]L #注意:不可以合写为 -Lniptables -n -L --line-numbers
3.设置默认策略:
iptables [-t 表名] -P <链名> <控制类型> iptables -P INPUT DROPiptables -P FORWARD DROP #一般在生产环境中设置网络型防火墙、主机型防火墙时都要设置默认规则为DROP,并设置白名单
4.删除规则:
iptables -D INPUT 2iptables -t filter -D INPUT -p icmp -j REJECT
注意:
1.若规则列表中有多条相同的规则时,按内容匹配只删除的序号最小的一条 2.按号码匹配删除时,确保规则号码小于等于已有规则数,否则报错 3.按内容匹配删数时,确保规则存在,否则报错5.清空规则:
iptables [-t 表名] -F [链名] iptables -F INPUTiptables -F
注意:
1.-F 仅仅是清空链中的规则,并不影响 -P 设置的默认规则,默认规则需要手动进行修改 2.-P 设置了DROP后,使用 -F 一定要小心! #防止把允许远程连接的相关规则清除后导致无法远程连接主机,此情况如果没有保存规则可重启主机解决 3.如果不写表名和链名,默认清空filter表中所有链里的所有规则七.规则的匹配
1.通用匹配
可直接使用,不依赖于其他条件或扩展,包括网络协议、IP地址、网络接口等条件。
协议匹配:-p 协议名地址匹配:-s 源地址、-d 目的地址 #可以是IP、网段、域名、空(任何地址)接口匹配:-i 入站网卡、-o 出站网卡
iptables -A FORWARD ! -p icmp -j ACCEPT iptables -A INPUT -s 192.168.80.11 -j DROPiptables -I INPUT -i ens33 -s 192.168.80.0/24 -j DROP
2.隐含匹配
要求以特定的协议匹配作为前提,包括端口、TCP标记、ICMP类型等条件。
端口匹配:--sport 源端口、--dport 目的端口#可以是个别端口、端口范围--sport 1000 匹配源端口是1000的数据包--sport 1000:3000 匹配源端口是1000-3000的数据包--sport :3000 匹配源端口是3000及以下的数据包--sport 1000: 匹配源端口是1000及以上的数据包注意:--sport 和 --dport 必须配合 -p <协议类型> 使用
iptables -A INPUT -p tcp --dport 20:21 -j ACCEPTiptables -I FORWARD -d 192.168.80.0/24 -p tcp --dport 24500:24600 -j DROP
TCP标记匹配:–tcp-flags TCP标记
iptables -I INPUT -i ens33 -p tcp --tcp-flags SYN,RST,ACK SYN -j ACCEPT#丢弃SYN请求包,放行其他包
ICMP类型匹配:–icmp-type ICMP类型
#可以是字符串、数字代码、、目标不可达“Echo-Request”(代码为 8)表示 请求“Echo-Reply”(代码为 0)表示 回显“Destination-Unreachable”(代码为 3)表示 目标不可达关于其它可用的 ICMP 协议类型,可以执行“iptables -p icmp -h”命令,查看帮助信息
iptables -A INPUT -p icmp --icmp-type 8 -j DROP #禁止其它主机ping 本机iptables -A INPUT -p icmp --icmp-type 0 -j ACCEPT #允许本机ping 其它主机iptables -A INPUT -p icmp --icmp-type 3 -j ACCEPT #当本机ping 不通其它主机时提示目标不可达#此时其它主机需要配置关于icmp协议的控制类型为 REJECTiptables -A INPUT -p icmp -j REJECT
3.显式匹配
多端口匹配:
要求以“-m 扩展模块”的形式明确指出类型,包括多端口、MAC地址、IP范围、数据包状态等条件。
多端口匹配:-m multiport --sports 源端口列表 -m multiport --dports 目的端口列表
iptables -A INPUT -p tcp -m multiport --dport 80,22,21,20,53 -j ACCEPT iptables -A INPUT -p udp -m multiport --dport 53 -j ACCEPT
IP范围匹配
IP范围匹配:-m iprange --src-range IP范围iptables -A FORWARD -p udp -m iprange --src-range 192.168.80.100-192.168.80.200 -j DROP #禁止转发源地址位于192.168.80.100-192.168.80.200的udp数据包
MAC地址匹配
MAC地址匹配:-m mac --mac-source MAC地址iptables -A FORWARD -m mac --mac-source xx:xx:xx:xx:xx:xx -j DROP#禁止来自某MAC 地址的数据包通过本机转发
状态匹配
状态匹配:-m state --state 连接状态常见的连接状态:NEW :与任何连接无关的,还没开始连接ESTABLISHED :响应请求或者已建立连接的,连接态RELATED :与已有连接有相关性的(如FTP 主被动模式的数据连接),衍生态,一般与ESTABLISHED 配合使用INVALID :不能被识别属于哪个连接或没有任何状态iptables -A FORWARD -m state --state NEW -p tcp ! --syn -j DROP#禁止转发与正常 TCP 连接无关的非--syn 请求数据包(如伪造的网络攻击数据包)
主机防火墙配置
iptables -I INPUT -p tcp -m multiport --dport 80,22,21,20,53 -j ACCEPTiptables -A INPUT -p udp -m multiport --dport 53 -j ACCEPT iptables -I INPUT -p tcp -m state --state ESTABLISHED,RELATED -j ACCEPTiptables -P INPUT DROP
八.DNAT原理与应用
1.DNAT 应用环境
- DNAT 应用环境:在Internet中发布位于局域网内的服务器
2.DNAT原理
- DNAT原理:修改数据包的目的地址。
3.DNAT转换前提条件
- 1.局域网的服务器能够访问Internet
- 2.网关的外网地址有正确的DNS解析记录
- 3.Linux网关开启IP路由转发
4.DNAT的打开方式
vim /etc/sysctl.confnet.ipv4.ip_forward = 1 sysctl -p
5.DNAT转换
DNAT转换1:发布内网的Web服务
#把从ens33进来的要访问web服务的数据包目的地址转换为 192.168.80.10iptables -t nat -A PREROUTING -i ens33 -d 12.0.0.1 -p tcp --dport 80 -j DNAT --to 192.168.133.10或iptables -t nat -A PREROUTING -i ens33 -d 12.0.0.1 -p tcp --dport 80 -j DNAT --to-destination 192.168.133.10 入站 外网网卡 外网IP 内网服务器IP iptables -t nat -A PREROUTING -i ens33 -p tcp --dport 80 -j DNAT --to 192.168.80.10-192.168.133.20
DNAT转换2:发布时修改目标端口
#发布局域网内部的OpenSSH服务器,外网主机需使用250端口进行连接iptables -t nat -A PREROUTING -i ens33 -d 12.0.0.1 -p tcp --dport 250 -j DNAT --to 192.168.80.10:22#在外网环境中使用SSH测试ssh -p 250 root@12.0.0.1yum -y install net-tools #若没有 ifconfig 命令可提前使用 yum 进行安装ifconfig ens33注意:使用DNAT时,同时还有配合SNAT使用,才能实现响应数据包的正确返回
小知识扩展:
主机型防火墙 主要使用 INPUT、OUTPUT 链,设置规则时一般要详细的指定到端口 网络型防火墙 主要使用 FORWARD 链,设置规则时很少去指定到端口,一般指定到IP地址或者到网段即可防火墙规则的备份和还原
导出(备份)所有表的规则iptables-save > /opt/ipt.txt
导入(还原)规则iptables-restore < /opt/ipt.txt
将iptables规则文件保存在 /etc/sysconfig/iptables 中,iptables服务启动时会自动还原规则iptables-save > /etc/sysconfig/iptablessystemctl stop iptables #停止iptables服务会清空掉所有表的规则systemctl start iptables #启动iptables服务会自动还原/etc/sysconfig/iptables 中的规则
转载地址:http://qseu.baihongyu.com/